UNIDADES DE MEDIDA DE UN ÁNGULO

a) Marco teórico

ANGULO

figura de la geometría que se forma a partir de dos rectas que se cortan entre sí en una 
misma superficie. También puede decirse que un ángulo está formado por dos 
semirrectas que comparten un mismo vértice.

LA UNIDAD DE LOS ANGULOS

pueden medirse en diferentes unidades: el grado sexagesimal y el radián son las medidas más frecuentes



Radian:unidad de medida de un angulo en S.I que equivale a un angulo plano que teniendo su verie en centro de la circunferencia, le corresponde un arco de la longitud igual al radio de la circunferencia
Angulo

Grado sexagesimal es el ángulo central subtendido por un arco cuya longitud es igual a 1/360 de la circunferencia. Es la nonagésima (1/90) parte de un ángulo recto.

como habíamos dicho anteriormente, los ángulos se pueden medir de 2 formas:el grado sexagesimal y en radianes, un circulo equivale a 2π radianes por lo cual tendremos estas conversiones.

π------->180°

2π------->360°

en base a esa conversión, se puede sacar la formula para convertir de grados a radianes o radianes a grados, la siguiente formula muestra esta conversión

con esa formula podemos convertir cualquier radian o grados a su contrariedad, a continuación se muestra un circulo con todos los radianes y grados que equivalen

FORMAS DE MEDIR UN ANGULO

POSITIVO Y NEGATIVO

Ángulos Positivos

Los ángulos positivos sobre el círculo se miden con la parte inicial en lo positivo eje "X" y el lado del terminal se mueve en sentido contrario a las manecillas del reloj a partir del origen. La figura muestra algunos ángulos positivos etiquetados en ambos grados y radianes.

Ángulos Negativos

 muchos de los ángulos básicos tienen valores negativos e incluso múltiplos de sí mismos. Si se mide ángulos hacia la derecha en vez de la izquierda, entonces los ángulos tienen medidas negativas:

Un ángulo de 30 grados es el mismo que un ángulo de medición de -330 grados, porque tienen el mismo lado terminal. Del mismo modo, un ángulo de

es lo mismo que un ángulo de

un ángulo de 60 grados tiene el mismo lado del terminal como la de un ángulo de 420 grados y un ángulo de -300 grados. La figura muestra muchos nombres para el mismo ángulo de 60 grados en ambos grados y radianes.

b) Introducción teórica

Sabemos que la longitud de la circunferencia viene dada `por la fórmula:

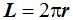
Sabemos también que un radián es un ángulo central cuya longitud de arco equivale al radio.
Si una circunferencia tiene una longitud de 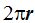y cada radián tiene una longitud de r (radio), el cociente: 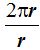será igual al número de radianes que tiene una circunferencia.Simplificando obtengo: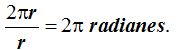

Se nos dio a la tarea de conseguir un objeto circular cuyo radio debíamos medir.Como resultado encontramos que 5 cm es la medida de el radio, ahora lo que debemos sacar es el resultado de los radianes que contiene esta circunferencia respecto a su radio.

Por lo anterior dicho y sustituyendo la forma ya mostrada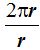 se t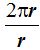iene que

6.2 radianes (tiras de color azul y negro) contiene esta circunferencia cuyo radio es de 5 cm.









  Aquí que se demuestra que teniendo el radio de cualquier medida el resultado siempre sera que contendrá 6.2 radianes (aproximadamente) en su circunferencia