PROBLEMAS ECUACIÓN DE LA RECTA

PROBLEMAS ECUACIÓN DE LA RECTA

https://docs.google.com/document/d/1L2l9pCTjRdx8kd_4iHEYUT8ULIAddroHEsuCTCJixTM/edit?usp=sharing

CALAVERA LITERARIA: "PITAGORAS Y EL DILEMA DE LA MUERTE""

PITÁGORAS Y EL DILEMA DE LA MUERTE

Estaba el matemático Pitágoras

Cuando de pronto entro la muerte,

La calaca  le dijo que había llegado su hora

Así que Pitágoras le advierte:

"Aun No puedo morir

Pues no he acabado mi teorema,

Solo dame mas tiempo de vivir,

Para solucionar muchos problemas"

La cansada  calaca triste

Se sienta a esperar

Pues el sabe que no existe

Un sabio que lo pueda ilustrar

De pronto la flaca se exalta

Pues matemáticas le falta

A su memoria le viene

La tarea a primera hora del viernes

  

El matemático comienza a burlar

Pues la hipotenusa debía calcular,

 Así que muerte la tenia que encontrar

Si el semestre no quería recursar

Después de una gran atormenta

Al fin la flaca entendió 

La muerte estaba muy contenta

Pues con Pitágoras el aprendió

Acabando el día se dio cuenta

Del difícil problema que comprendió

 La muerte a cambio

Del gran aprendizaje

Le dejo una carta al sabio

Con el siguiente mensaje:

  

"Mi buen maestro Pitágoras

Espero que concluyas tu teorema

Pues ya llevas muchas horas

Con esos feos problemas,

Pero te a seguro que seras necesitado

Por muchos alumnados

Que acudirán a tu ecuación

Con mucha desesperación"

"Solo te doy las gracias

Por el conocimiento dado

Y dada las circunstancias

Vengo después como has anhelado"

"Pues ahora por fin, no voy a reprobar

Como ya lo había esperado

Solo me queda ir a triunfar 

Con el conocimiento que me has dado"

RECTAS, PUNTOS NOTABLES Y CENTRO DE GRAVEDAD DE UN TRIANGULO.

RECTAS Y PUNTOS NOTABLES DE UN TRIANGULO

Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. En los triángulos se puede denotar un grupo de rectas y puntos muy importantes. Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

Por consiguiente se muestran las rectas y puntos notables de un triangulo.

ALTURA-ORTOCENTRO

Altura: La altura de un triángulo, respecto de uno de sus lados, se define como la recta perpendicular a dicho lado que pasa por el vértice opuesto.


Ortocentro: Es el punto intersección de las tres alturas de un triángulo.

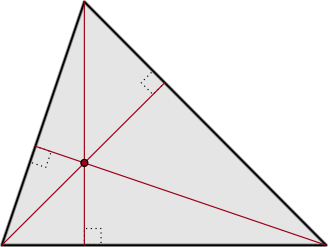
MEDIANAS-BARICENTRO

Mediana: Las medianas de un triángulo, correspondiente a uno de sus vértices, se define como la Recta que pasa por el punto medio de un lado y el vértice opuesto a ese lado.

Baricentro: Es el punto de corte de las tres mediana.

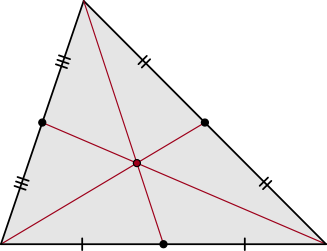
BISECTRIZ-INCENTRO

Bisectriz: La bisectrizde un triángulo, correspondiente a uno de sus vértices, se define como la recta que, pasando por dicho vértice, divide ángulo interior correspondiente en dos partes iguales.


Incentro: Es el punto en el que se cortan las tres bisectrices de los ángulos internos del triángulo, y es el centro de lacircunferencia inscrita en el triángulo y que equidista de sus tres lados, siendo tangente a dichos lados.

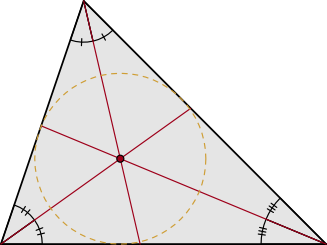
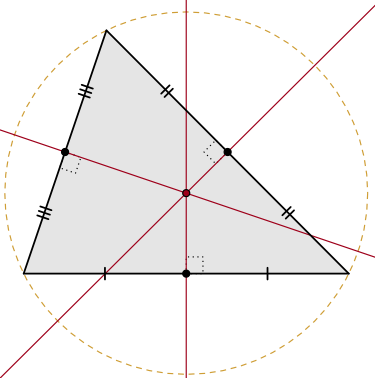
MEDIATRIZ-CIRCUNCENTRO

Mediatriz: La mediatriz de un lado de un triángulo se define como la Recta que pasa por el punto medio de un lado y perpendicular a éste.


Circuncentro: Es el punto en el que se intersectan las tres mediatrices de un triángulo y es el centro de la circunferencia circunscrita

  

HALLAR EL PUNTO DE GRAVEDAD DE UN TRIANGULO

El centro de gravedad de un triangulo o tambien conocido  como centroide es llamado al punto que intersectan las rectas medianas o llamado baricentro, y esta siempre se lozalizara en el interior de el triangulo, por lo dicho antes se cumple la siguiente propiedad: la distancia entre el baricentro (centroide) y su vértice correspondiente es el doble de la distancia entre el baricentro y el lado opuesto. Es decir, la distancia del centroide a cada vértice es de 2/3 la longitud de cada mediana.

Asi que el objetivo de este trabajo es el localizar el centro de gravedad de un triangulo cualesquiera medidas.

Geometricamente

1.-Encontrar o crear un triangulo hecho de material rígido (plastico, madera, carton, vidrio).

2.-Trazar un plano cartesiano sobre una hoja de papel, con las medidas que usted quiera.

3.-Colocar el triangulo rígido sobre el pano y trazar su contorno.

4.-Ubicar y anotar las coordenadas de los vértices de la figura.En este caso las coordenadas del vértice son las siguientes.

   

teniendo todo esto, procederemos a encontrar el centro de gravedad, con el método analítico

Analíticamente

recordemos que para localizar el centro de gravedad, nos apoyaremos con los trazos de las medianas, por lo que debemos dividir el segmento a la mitad, así que nos ayudaremos ocupando la siguiente formulas:

La formula ya mostrada nos ayuda a dividir un segmento dada una razón ya establecida, en este caso como queremos dividir el segmento a la mitad (punto medio), le daremos a la razon un valor de "1".

Posteriormente seleccionaremos las coordenadas de los extremos del segmento que queremos dividir y le asignaremos la referencia:

En conclusión las dos formulas nos ayudaran a encontrar las coordenadas del punto medio en forma X,Y, por lo que repetiremos este procedimiento con los 3 segmentos o lados de el triangulo.

                                                     ahora solo queda sustituir los valores.

Punto medio del segmento AB

                                                                                   

                          

coordenadas

 del punto medio AB

(-3.95, 1.5)

mediana

Punto medio del segmento AC

 

 

 

coordenadas

 del punto medio AC

(-0.75, 4.4)

mediana

Punto medio del segmento CB

coordenadas

 del punto medio CB

(1.29, 0.4)

mediana

Ahora solo nos queda ubicar las coordenadas de el punto medio de los 3 segmentos en el plano cartesiano, y posteriormente unir el punto medio con el vértice opuesto a ese lado para asi poder trazar la mediana de dicho segmento.

Este procedimiento lo repetimos con los demás puntos medios y vértices del triangulo.El punto que intersectan estas tres medianas, se llama baricentro, y es el centro de gravedad de nuestro triangulo. limitado en este caso en las coordenadas:

Baricentro ----------------->

Ahora estas lineas las trazaremos en el triangulo rígido que hemos escogido.

Para comprobar que el centroide esta correctamente ubicado procederemos a colocar una base con un una pluma en forma vertical, y posicionaremos la punta en el baricentro del triangulo.


             

Si realizamos el trabajo de formal correcta, observaremos al triangulo que logra equilibrarse de forma estática en la punta de nuestra pluma, cuando veamos que no caiga; ¡felicidades haz encontrado en centro de gravedad de tu triangulo!.